Continuing the series on lasers. In the first part, I went fast over plenty of concepts and left others on the side because they were not necessary to get a global understanding of lasers. Here, I want to get a little deeper in some specific concepts. I want to talk more in details about the gain medium of a laser and why population inversion is a vital concept.
For now, I have been relatively simple on the gain medium characteristics… I have considered a simple material with two atomic energy levels, and I have been assuming that the transition is the laser transition… In reality, things are much more complicated than that.
Gain mediums have several atomic levels, most of them not able to lase because of the lifetime of the state or because of the energy difference between them. Another point I simplified is that I took into consideration just one electron being on an excited state. In a real gain medium, there is a given number of electron, usually written N underscore something, that describes how many electrons are excited in the given atomic level. Typically, you will have in an excited gain medium several atomic levels, each with a given amount of excited electrons ready to make a transition to some other atomic level.
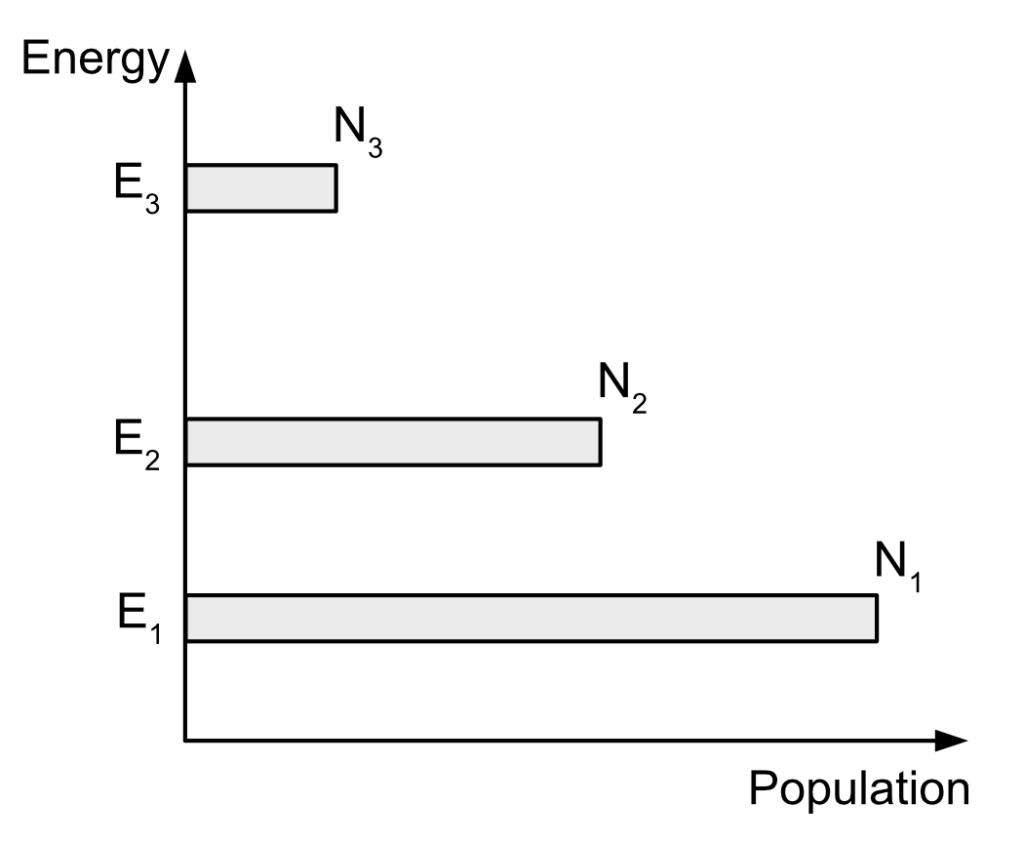
It can become pretty quickly hard to follow what is happening and how to describe things if we keep talking about it in a written form. So unfortunately, to better describe what is happening, I’ll have to use some mathematical relations, in particular differentials equations.
The first thing to know is that the rate of variation of a population level can be written in this form:
\dfrac{dN(t)}{dt}=-1/\tau\times N(t)
Where N is the number of electron in the level considered and \tau is the lifetime of the electron in that level.
What does that mean ? It effectively means that the more electrons are on that atomic level, the faster they leave that level. \dfrac{dN(t)}{dt} is the variation rate of the population of electrons, how many electrons leave the atomic level in an amount of time dt. And we can see that the higher the lifetime $\tau$ of that level, the lower that rate becomes. We can also see that the higher the amount of electrons on that atomic level, the higher the rate and the faster the level depletes.
This is typically how we would write spontaneous emission in mathematical form.
If we were to plot the function N against time, that is to say the evolution of the amount of electron in the atomic level, we would get an exponential like this:
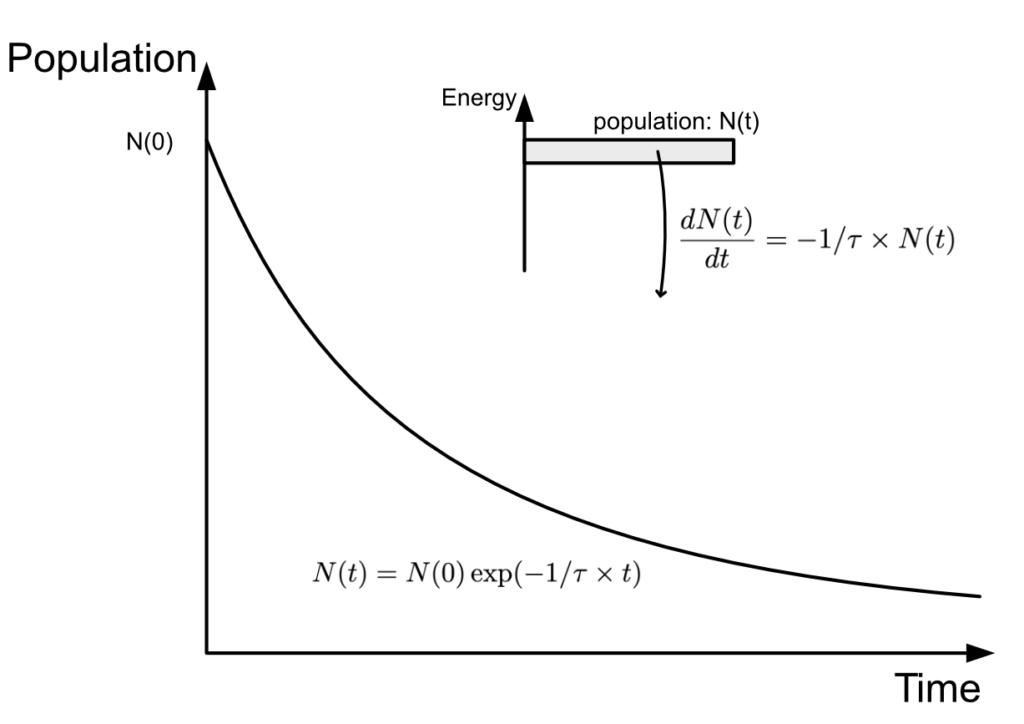
This equation works for when electrons leave an atomic level. This is good, but how to describe the act of pumping, that is to say adding electrons to an atomic level?
We simply change the sign in the differential equation because the level 2 is going to gain electrons and obtain:
\dfrac{dN_2(t)}{dt}=K\times n(t) \times N_1(t)
Where K is the pumping rate and n(t) is the amount of photons travelling in the gain medium. It can be seen as the laser intensity. As you can see here, we have two different Ns. N_1 and N_2, N_1 corresponding to the amount of electrons in the first energy level (level 1), from where the pumped electrons will come from and N_2 corresponding to the amount of electrons in the energy level where the pumped electrons will go (level 2).
Again, what does that equation means? It means that the rate with which the amount of electrons in the destination atomic level is proportional to the pumping rate times the amount of electrons in the initial atomic level. The more intensely we are pumping, the more electrons will flow to the level 2 from the level 1. It also means that the less they are electrons in the level 1, the slower the pumping process will become. Indeed, N_1 does not stay constant and varies with time as we are taking electrons away to put them in the level 2…
How do we describe the stimulated emission from the level 2 to the level 1?
\dfrac{dN_2(t)}{dt}=-K\times n(t) \times N_2(t)
Why do I talk about all of this?
You might remember in my first post that I explain how stimulated emission works and is at the basis of lasers. One point is crucial: If we have plenty of atoms at “rest” in the gain medium, won’t all the photons emitted by the lasing process be “cannibalized” by these atoms? How can we have amplification in that case if most of the photons are use to raise the electronic state of ground atoms?
Ah. That is an interesting question.
Let’s consider the variation of the population of the level 2 in a two level gain medium.
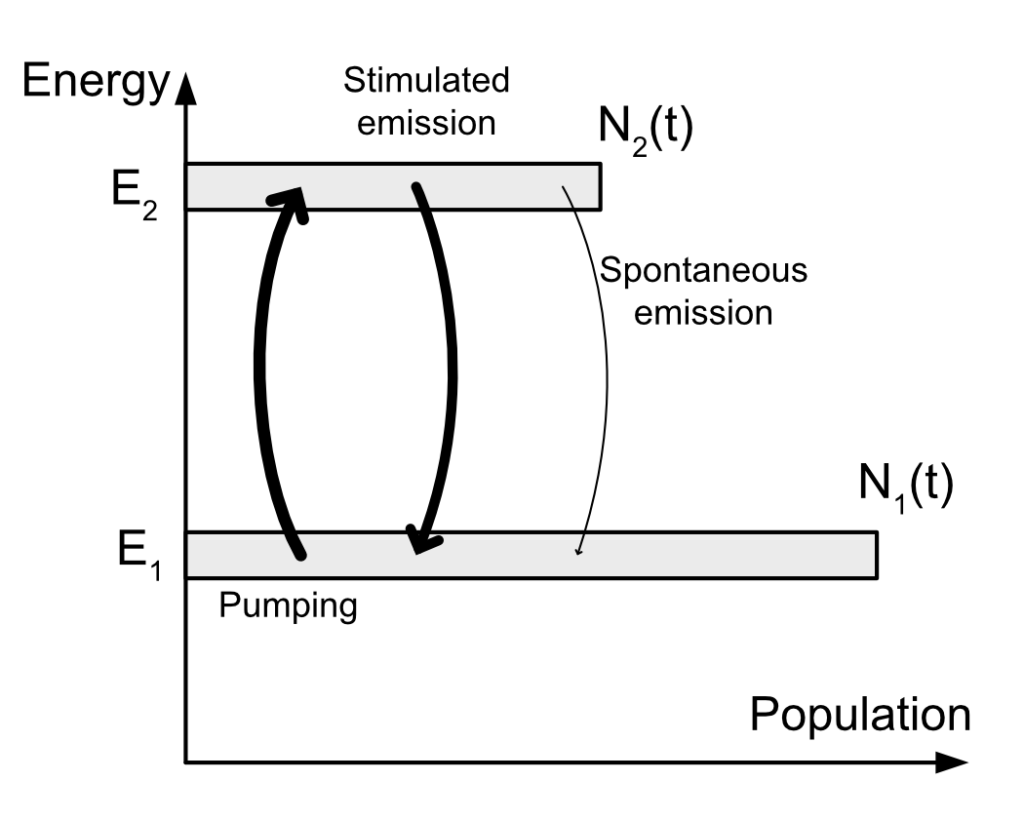
We have electrons coming to the level 2 via pumping and we have electrons leaving the level 2 via stimulated emission and via spontaneous emission. We can write this whole sentence mathematically like this:
\dfrac{dN_2(t)}{dt}=\underbrace{Kn(t)N_1(t)}_\text{pumping}\overbrace{-Kn(t)N_2(t)}^\text{stimulated emission}\underbrace{-1/\tau N_2(t)}_\text{spontaneous emission}
That easily becomes:
\dfrac{dN_2(t)}{dt}=Kn(t)(N_1(t)-N_2(t))-1/\tau N_2(t)
From this equation, we see the dynamics between two atomic levels, how electrons move from level 1 to level 2, and from level 2 to 1, consuming or emitting a photon in the process.
But in lasers, we are actually more interested with the amount of photons in the system, that is to say, how n(t) varies with time.
It turns out that n(t) can be written in this form as well:
\dfrac{dn(t)}{dt} = -Kn(t)N_1(t)+Kn(t)N_2(t)+1/\tau N_2(t)
Because for each electronic transition from level 2 to 1 and from level 1 to 2, there is either a photon released (n(t) increases) or a photon absorbed (n(t) decreases) respectively.
Because we consider ourselves in a situation where the medium is lasing, we can forget about the spontaneous emission term that is going to be orders of magnitude smaller than the other stimulated emission terms and get:
\dfrac{dn(t)}{dt} \approx -Kn(t)(N_1(t)-N_2(t))
From this equation, we see that if we want to see n(t) increase with time, that is to say, if we want to create more and more photons and see true light amplification, we need the other side of the equation to be positive. We can only have that other side of the equation positive if N_2>N_1 because K and n(t) are positive numbers.
This condition is called the population inversion condition and it is the most important condition for a functioning laser system.
This population inversion is not common in normal atomic systems and I’ll describe in another post how it is achieved in practice.