Continuing my series of post covering my talk from last Christmas about the use of lasers in space and astronomy. The topic today is adaptative optics. I’ll explain the reason why we need it, and how it works in simple terms. Enjoy.
No surprise: telescopes are the main tool of astronomers. Since Newton, we have built countless telescopes of various sizes and shapes. And lately, we even send them to space. We have Hubble, the JSWT for the more famous, and a lot of other space telescopes less known. But why sending them to space? After all, space is difficult. The telescope is far away for maintenance if necessary. Communication and data transfert is a challenge. Moreover, we can’t send “heavy” mirrors, rockets can only cary a certain amount of weight, and it is not a lot.

The reason we still send telescopes in space might be obvious: we want to avoid the earth’s atmosphere. As it turns out, we do not notice that the atmosphere is not transparent nor that it is heavily disturbed in ways that make imaging a chalenge. Over the several kilometres that make the thickness of the various layers of the earth’s atmosphere are several issues, that make imaging difficult.
First, on the sea level, we have thermal perturbations. During the day, the sun heats the landscape and at night, different parts of the landscape will emit heat in a way or another. Rocks, fields, forests, lakes, all have their own ways to re-emit this heat, creating currents with various densities in the atmosphere.
Then we have the effect of the relief on the air flow. Mountains tend to modify the flow of air around them, and creates more turbulent flow. Finally, higher up, we have the jet stream, a high velocity wind that also tends to disrupt imaging through it.
All these contribute in making the atmosphere very difficult for imaging. The effect is actually well known to most people, as the kid song says “Twinkle, twinkle, little star…”. The “twinkling” is the effect cause by the perturbations in the atmosphere: the turbulences. It makes the star move around, and even can cause chromatic effects. This is particularly noticeable for stars that are low on the horizon because light has to cross a larger amount of atmosphere before reaching us.
And of course, we also understand that the turbulences are going to prevent us from making high resolution imaging at sea level. Because we already don’t have much light to do the imaging, astrophotography requires the use of long exposures. Because the target moves randomly because of the turbulences, the resolution is limited. This is called the “seeing”, and it is crucial to take nice images of the sky.
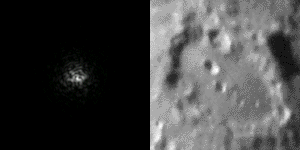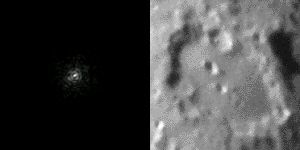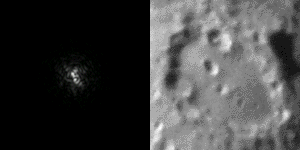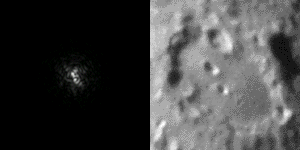
So if we have lot of atmosphere, we have lot of turbulence and low resolution. The solution is simple: if we have little atmosphere, we have little turbulences and high resolution. This is true and it is the reason why most big telescopes are built in the Atacama desert, and other high plateau around the world, avoiding a large portion of the turbulent atmosphere certainly helps to get nice images. And obviously, space is the ultimate place as there is no atmosphere…

Still. Space is difficult and expensive. What if we could analyse and compensate these turbulences in the atmosphere? This is the idea behind adaptive optics. And to understand it, we need to go deeper in the reason why the turbulent atmosphere is preventing us from making nice images.
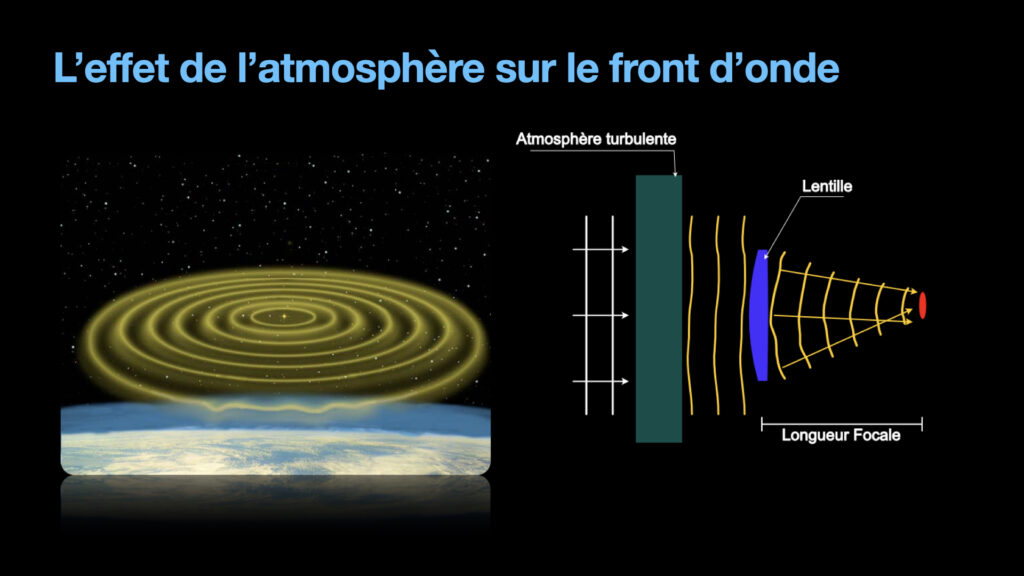
We need to understand two key concept: the wavefront of light and how a telescopes bends the wavefront to make an image. Let’s start with the wavefront of light. A star is going to emit light in all directions. In geometric optics, we can model this by spherical waves, where the center is the star. These waves propagate in space, the same way a wave caused by a rock thrown in a lake creates ripples moving along the surface of the lake. The summit of those ripples, the maximum of the wave is drawing circles in the lake. It is the wavefront of the ripple. Light propagates in 3D, therefore, the wavefront is a sphere with the start at its center. Because we are so far away from the star and only intercepting an infinitesimal portion of the wavefront, the spherical wavefront from the distant star can be simplified in a plane wavefront, that is a sphere with infinite radius.


Now, how telescopes work? The basic idea is that the telescope is going to catch part of this planar wavefront and bend it, to create a new spherical wavefront, with the new center of the wavefront on the surface of some sensor, be it a camera or our retina. This is actually the purpose of the lens in a telescope, or the mirror depending on the type of telescope. The lens or mirror are designed to be focusing a perfect planar wavefront.
And when our atmosphere is turbulent, the planar wavefront actually gets distorted. Patches of the atmosphere appear denser, which means that light is propagating more slowly, which effectively distort the front. The lenses being designed to focus a perfect planar wavefront, the result is a blurry focusing spot. And because the atmosphere is changing all the time, the blurry focusing spot changes shape all the time and creates this twinkling effect.
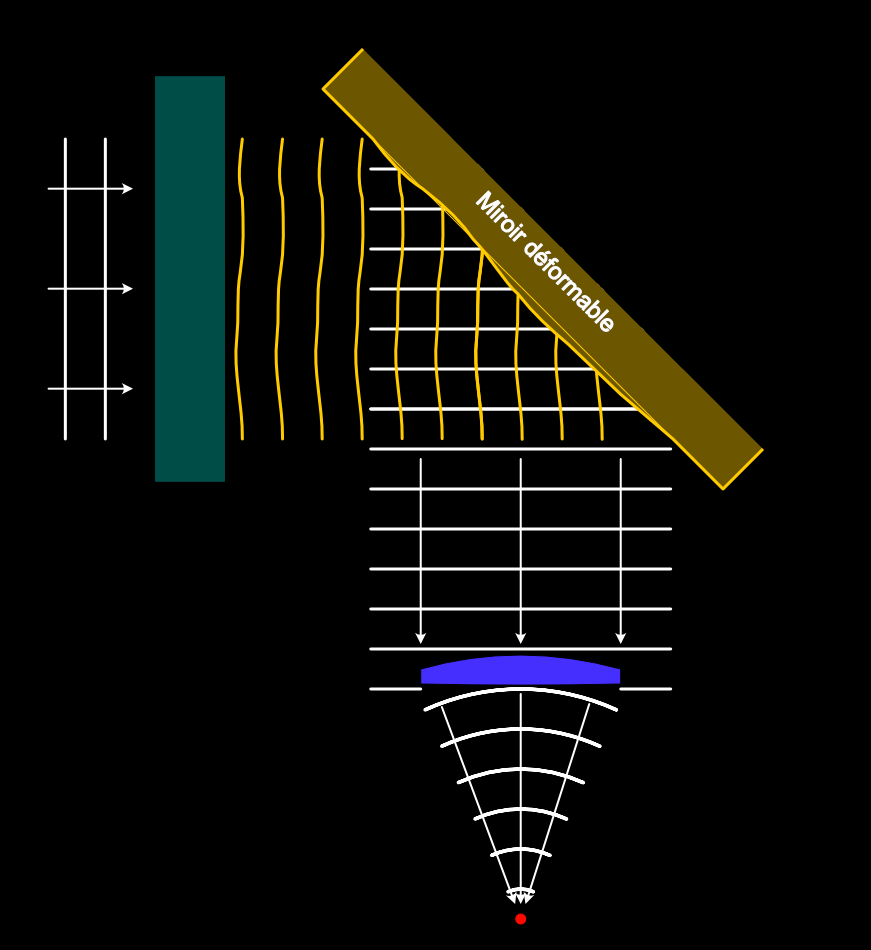
Adaptative optics is simple: if we know the turbulence that the planar wavefront goes through, we can insert a deformable mirror and have light reflect from it so that the reflection will be a planar wavefront again. The lens or mirror of the telescope will then focus the light as intended in a perfect spot.
So the question is now: How do we measure the turbulences? We need to have a reference. Something that we know for sure to emit a planar wavefront. One easy way to make that reference is to use an existing star. It is possible, but it also makes a difficult requirement that for the adaptative optics to work, a very bright star has to be present close to the portion of the sky to image. It is not convenient at all. So we need to create artificial stars. This is the goal of the lasers that one can see sometimes on time lapses for these large observatories. You can sometimes see these yellow lasers shooting to the sky. Each of these lasers are tens of Watts of power, with a wavelength corresponding to the sodium absorption line. The goal is to target a portion of the sky far above every turbulent layers, called the sodium layer. It is only a few kilometres thick at approximately 100 km of altitude. This layer has a higher concentration of sodium atoms compared to the rest of the atmosphere.
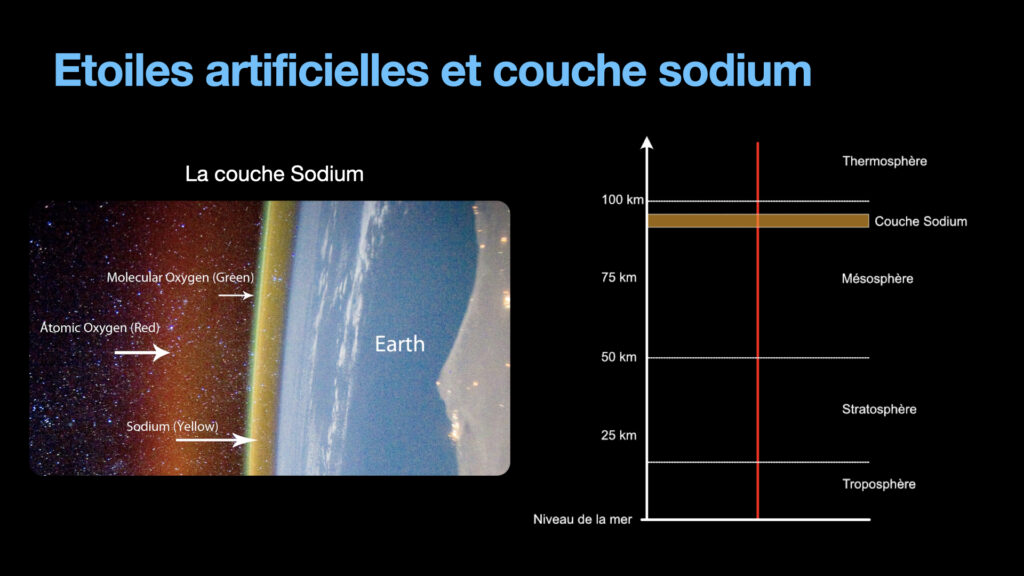
So the telescope is going to shoot the laser toward this sodium layer. Sodium atoms there will absorb the photons because they are at the exact right transition for these atoms. A little after, the excited atoms will re-emit the photons, in a random direction. Meaning that some part of the photons will come back toward the telescope. Those photons are enough to simulate a star of magnitude 6, which is the limit visible by the human eye, but enough for the adaptive optics.

Because those photons from the sodium layer are coming from the same part of the sky, small enough to simulate a star, we know that the wavefront from those photons is a plan. Therefore, the wavefront measured on earth is a direct representation of all the turbulences that exist between this fake sodium star and the telescope.
Now, it is the matter of how to measure the wavefront. For this, we use a device called a Shack-Hartmann sensor. To understand how it works, let’s start with a simple lens and a sensor. The lens is going to focus a planar wavefront on a focal point in the focal plane of that lens, where the sensor is. If the wavefront direction is perpendicular to the lens, then the focal position is in the optical axis and defines the center of the sensor cell. If the wavefront comes with a tilt, then the lens is going to focus the wavefront off-center. The distance between the center of the sensor and the position of the off-center focal spot is a representation of how the wavefront is distorted. The more it is tilted and therefore distorted, the further away the spot is from the center of the sensor.
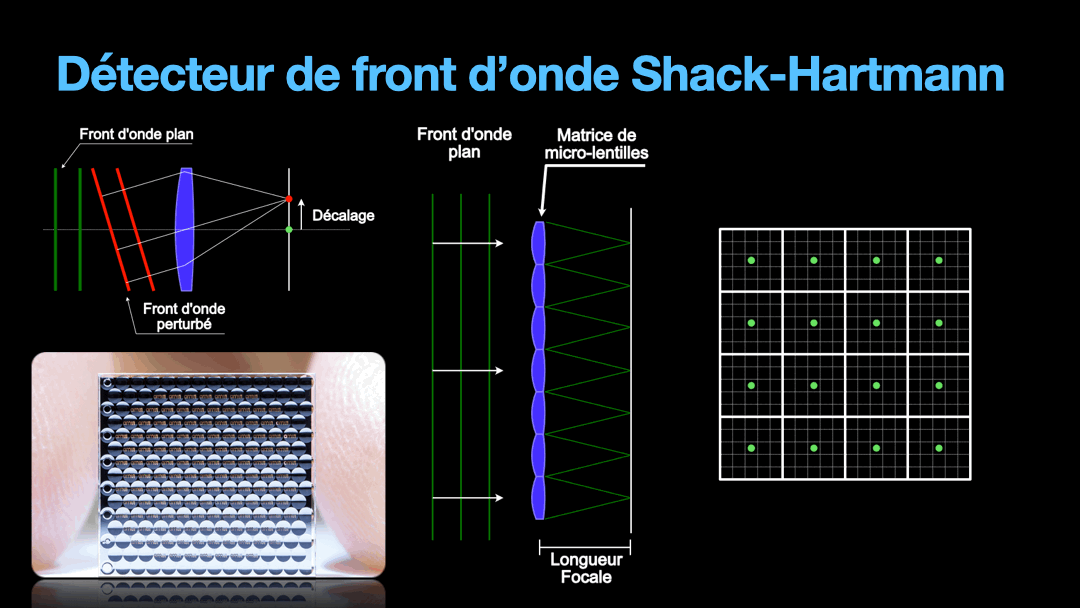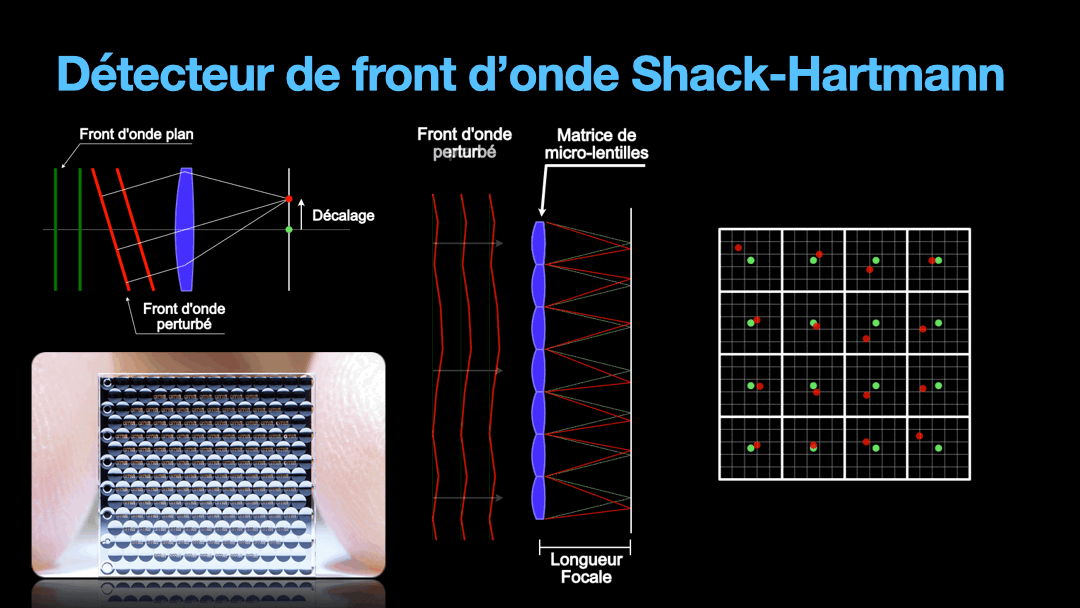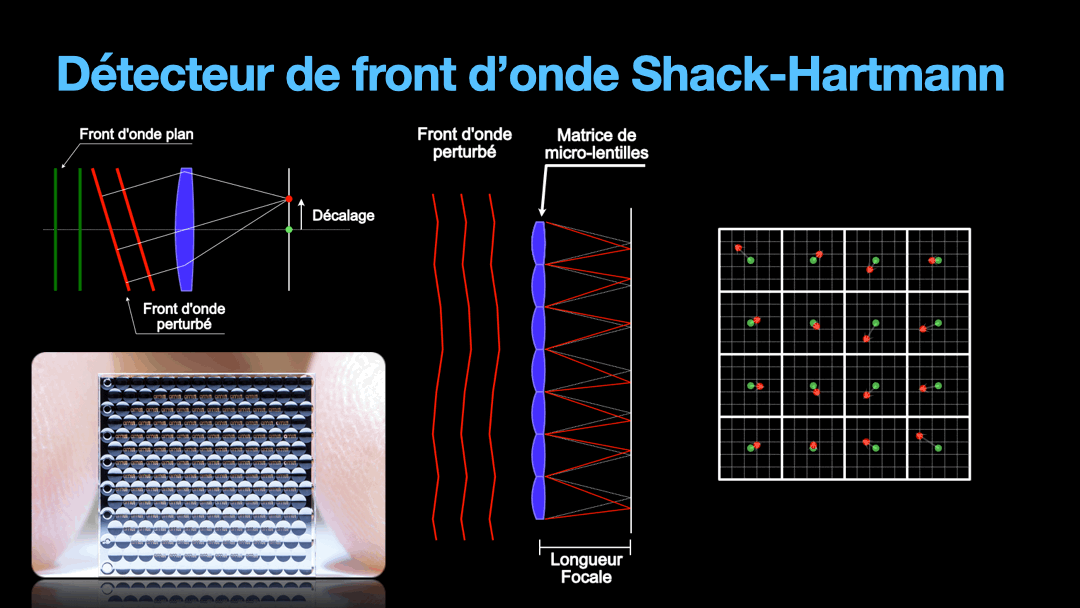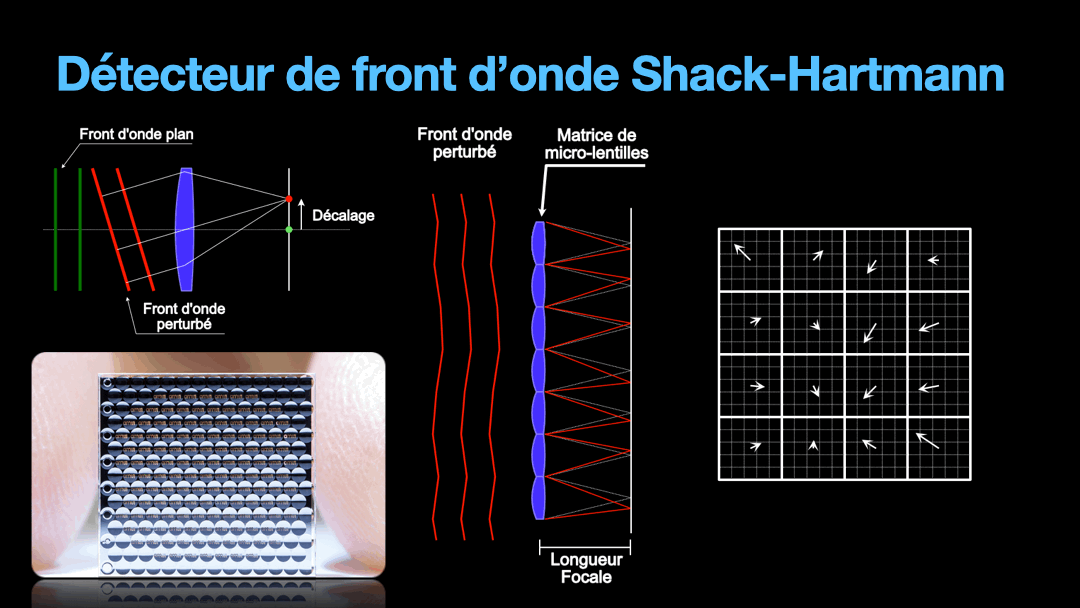
But we need to remember that the wavefront is a plane. And the distortion on that plane can get very random. So we are going to divide this plane into tiny section, each section will be imaged by a tiny lens from what is called a micro-lens array. Under each micro-lens, we have a cell that is going to represent the direction of the portion of the wavefront that fall upon it. This is the Shack-Hartmann sensor and how it works very simplistically.
Then, the information from the distortion of the wavefront is sent to actuators under a deformable mirror that is going to compensate the wavefront and correct the turbulences from the atmosphere. The result is that the images we can have on the telescopes on earth are very similar to what we can get in space, for less price and less trouble.
So why spending a fortune for the JWST? The atmosphere still. Because if we can solve the problem caused by the turbulences, we can’t solve the lost information caused by the atoms of the atmosphere. IR imaging, high energy imaging for instance are heavily disturbed by the atmosphere because the atoms of oxygen, nitrogen and the other compounds of the atmosphere capture a good amount of the light at some wavelengths that could be of interest for the astronomers…
Sources
https://elt.eso.org/telescope/adaptiveoptics/
https://en.wikipedia.org/wiki/Adaptive_optics
https://www.rp-photonics.com/laser_guide_stars.html
https://www.atnf.csiro.au/outreach/education/senior/astrophysics/atmosphere.html
